Cornelia Van Cott
Professor
Department of Mathematics & Statistics
University of San Francisco
Research Publications
Moshe Cohen, Thomas Kindred, Adam M. Lowrance, Patrick D. Shanahan, and Cornelia A. Van Cott. Submitted. Posted on arxiv.
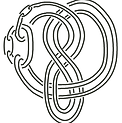
Abstract: We determine a simple condition on a particular state graph of an alternating knot or link diagram that characterizes when the unoriented genus and crosscap number coincide, extending work of Adams and Kindred. Building on this same work and using continued fraction expansions, we provide a new formula for the unoriented genus of a 2-bridge knot or link. We use recursion to obtain exact formulas for the average unoriented genus and average crosscap number of all 2-bridge knots with crossing number c.
Cornelia A. Van Cott and Qiyu Zhang. Discrete Mathematics. 349 (2026) no. 1, 19 pages.
Abstract: The change-making problem asks: given a positive integer v and a collection C of integer coin values c_1=1<c_2< c_3< ...< c_n, what is the minimum number of coins needed to represent v with coin values from C? For some coin systems C, the greedy algorithm finds a representation with a minimum number of coins for all v. We call such coin systems orderly. However, there are coin systems where the greedy algorithm fails to always produce a minimal representation. Over the past fifty years, progress has been made on the change-making problem, including finding a characterization of all orderly coin systems with 3, 4, and 5 coin values. We characterize orderly coin systems with 6 coin values, and we make generalizations to orderly coin systems with n coin values.
Cornelia A. Van Cott and Katie Wang. Involve, 17 (2024), no. 4, 669–687.
Abstract: We investigate the mathematics behind unshuffles, a type of card shuffle closely related to classical perfect shuffles. To perform an unshuffle, deal all the cards alternately into two piles and then stack the one pile on top of the other. There are two ways this stacking can be done (left stack on top or right stack on top), giving rise to the terms left shuffle (L) and right shuffle (R), respectively. We give a solution to a generalization of Elmsley's Problem (a classic mathematical card trick) using unshuffles for decks with 2^k cards. We also find the structure of the permutation groups generated by L and R for a deck of 2n cards for all n. We prove that the group coincides with the perfect shuffle group unless n is 3 modulo 4, in which case the group is equal to B_n, the group of centrally symmetric permutations of 2n elements, while the perfect shuffle group is an index 2 subgroup of B_n.
Jim Hoste, Patrick D. Shanahan, and Cornelia A. Van Cott, Journal of Knot Theory and Its Ramifications. 32 (2023), no. 5, 30 pages.
Abstract: We investigate the nonorientable 4-genus γ_4 of a special family of 2-bridge knots, the twist knots and double twist knots C(m,n). Because the nonorientable 4-genus is bounded by the nonorientable 3-genus, it is known that γ_4 (C (m, n)) ≤ 3. By using explicit constructions to obtain upper bounds on γ_4 and known obstructions derived from Donaldson’s diagonalization theorem to obtain lower bounds on γ_4, we produce infinite subfamilies of C(m,n) where γ_4 = 0, 1, 2, and 3, respectively. However, there remain infinitely many double twist knots where our work only shows that γ_4 lies in one of the sets {1, 2}, {2, 3}, or {1, 2, 3}. We tabulate our results for all C(m, n) with |m| and |n| up to 50. We also provide an infinite number of examples which answer a conjecture of Murakami and Yasuhara.
Jim Hoste, Patrick D. Shanahan, and Cornelia A. Van Cott, Journal of Knot Theory and Its Ramifications. 30 (2021), no. 4, 20 pages.
Abstract: We consider the relationship between the crosscap number, gamma, of knots and the partial order on the set of all prime knots, which is defined as follows. For two knots K and J, we say K ≥ J if there exists an epimorphism on the fundamental group of the knot exterior of K to that of J. We prove that if K and J are 2-bridge knots and K> J, then gamma(K) ≥ 3gamma(J) -4. We show that the inequality is sharp and that it does not hold in general for all prime knots. A similar result relating the genera of two knots has been proven by Suzuki and Tran. Namely, if K and J are 2-bridge knots and K >J, then g(K) ≥ 3 g(J)-1, where g(K) denotes the genus of the knot K.
Samuel Johnson, Lakshman Manny, Cornelia A. Van Cott, and Qiyu Zhang, Involve, 14 (2021), no. 5, 813–828.
Abstract: Standard perfect shuffles involve splitting a deck of 2n cards into two stacks and interlacing the cards from the stacks. There are two ways that this interlacing can be done, commonly referred to as an in shuffle and an out shuffle, respectively. In 1983, Diaconis, Graham, and Kantor determined the permutation group generated by in and out shuffles on a deck of 2n cards for all n. Diaconis et al. concluded their work by asking whether similar results can be found for so-called generalized perfect shuffles. For these new shuffles, we split a deck of mn cards into m stacks and similarly interlace the cards with an in m-shuffle or out m-shuffle (denoted I_m and O_m, respectively). In this paper, we find the structure of the group generated by these two shuffles for a deck of m^k cards, together with m^y-shuffles, for all possible values of m, k, and y.
Stanislav Jabuka and Cornelia A. Van Cott, Journal of Knot Theory and Its Ramifications, 29 (2020), no. 3, 15 pages.
Abstract: We compare the values of the nonorientable three genus (or crosscap number) and the nonorientable four genus of torus knots. In particular, we show that the difference between these two invariants can be arbitrarily large. This contrasts with the orientable case: Seifert proved in 1935 that the orientable three genus of the torus knot T(p, q) is (p-1)(q-1)/2, and subsequently in 1993, Kronheimer and Mrowka proved that the orientable four genus of T(p, q) is also this value.
Stanislav Jabuka and Cornelia A. Van Cott, Algebr. Geom. Topol. 21 (2021), no. 5, 2571–2625.
Abstract: The nonorientable 4-genus of a knot K is the smallest first Betti number of any nonorientable surface properly embedded in the 4-ball, and bounding the knot K. We study a conjecture proposed by Batson about the nonorientable 4-genus for torus knots, which can be seen as a nonorientable analogue of Milnor's Conjecture for the orientable 4-genus of torus knots. We prove the conjecture for many infinite families of torus knots, by relying on a lower bound formulated by Ozsvath, Stipsicz, and Szabo. As a side product we obtain new closed formulas for the signature of torus knots.
Charles Livingston and Cornelia A. Van Cott, Mathematical Proceedings of the Cambridge Philosophical Society, 164, (2018), no. 3, 531 - 550.
Abstract: We study the four-genus of linear combinations of torus knots: aT (p, q )# -bT (p',q'). Fixing positive p, q, p', and q', our focus is on the behavior of the four-genus as a function of positive a and b . Three types of examples are presented: in the first, for all a and b the four-genus is completely determined by the Tristram-Levine signature function; for the second, the recently defined Upsilon function of Ozsvath-Stipsicz-Szabo determines the four-genus for all a and b ; for the third, a surprising interplay between signatures and Upsilon appears.
James Gagne, Andrew Van Cott, and Cornelia A. Van Cott, Integrated Environmental Assessment and Management, 14, (2018), no. 6, 703 - 709.
Abstract: Calculating pesticide residue levels in feed items for terrestrial species requires accounting for the application rate of the pesticide, the frequency and interval of application, the half-life of the pesticide on the food item, and the residue unit dose. Microsoft Excel™–based applications such as the US Environmental Protection Agency's Terrestrial Residue Exposure model (T-REX) and Terrestrial Herpetofaunal Exposure Residue Program (T-HERPS) calculate the residue levels in feed items using a recursive sequence. A recursive sequence is an unwieldy calculation method that presents a barrier to creating a software-based tool capable of conducting flexible assessments. Therefore, we determined the closed form of the recursive mathematical equation used by both T-REX and T-HERPS. With this formula, we can both duplicate screening-level assessments (T-REX, T-HERPS) as well as incrementally refine the assessment with data-driven inputs.
Cornelia A. Van Cott, Journal of Knot Theory and its Ramifications, 22 (2013), no. 6, 10 pages
Abstract: Recent advances in understanding slicing properties of Bing doubles of knots have depended on properties of iterated covering links. We expand and refine this covering link calculus. Our main application here is a simplified proof of the following result of Cha and Kim: If the iterated Bing double of a knot K is slice, then K is algebraically slice. Further applications are included in joint work with Livingston studying 4-genera of Bing doubles. The techniques also appear in the work of Adam Levine studying mixed Bing-Whitehead doubles.
Cornelia A. Van Cott, Algebraic & Geometric Topology, 10 (2010), 825 - 836.
Abstract: We study the behavior of the Ozsvath--Szabo and Rasmussen knot concordance invariants K(m,n), the (m,n)-cable of a knot K where m and n are relatively prime. We show that for every knot K and for any fixed positive integer m, both of the invariants evaluated on K(m,n) differ from their value on the torus knot T(m,n) by fixed constants for all but finitely many n>0. Combining this result together with Hedden's extensive work on the behavior of the Ozsvath--Szabo invariant on (m,mr+1)-cables yields bounds on the value of the invariant on any (m,n)-cable of K. In addition, several of Hedden's obstructions for cables bounding complex curves are extended.
Charles Livingston and Cornelia A. Van Cott, Mathematical Proceedings of the Cambridge Philosophical Society, 151 (2011), 459 - 470.
Abstract: Cha and Kim proved that if a knot K is not algebraically slice, then no iterated Bing double of K is concordant to the unlink. We prove that if K has nontrivial signature, then the nth-iterated Bing double of K is not concordant to any boundary link with boundary surfaces of genus less than 2^{n-1}*signature. The same result holds with signature replaced by twice the Ozsvath-Szabo knot concordance invariant.
Cornelia A. Van Cott, Algebraic & Geometric Topology, 7 (2007), 181 - 196.
Abstract: For a knot K, let l(K,n) be the minimum length of an n-stranded braid representative of K. Fixing a knot K, l(K,n) can be viewed as a function of n, which we denote by l_K(n). Examples of knots exist for which l_K(n) is a non-increasing function. We investigate the behavior of l_K(n), developing bounds on the function in terms of the genus of K. The bounds lead to the conclusion that for any knot K the function l_K(n) is eventually stable. We study the stable behavior of l_K(n), with stronger results for homogeneous knots. For knots of nine or fewer crossings, we show that l_K(n) is stable on all of its domain and determine the function completely.
Publications for General Audiences
Cornelia A. Van Cott, Math Horizons, 28 (2021) no. 2, 24 - 27.
Abstract: Without hands, feet, or hips, most of the hokey pokey dance is out of reach for our numerical friends, the integers. But, what about the ending – the part of the dance where “you turn yourself around”? Twentieth century mathematician G.H. Hardy in his famed essay A Mathematician’s Apology pointed out two integers that can turn themselves around, in a sense. These numbers are 1089 and 2178. We set out on a quest to find all such integers, and we encounter surprising structure along the way.
The Mathematical Association of America awarded this paper the 2021 Trevor Evans Award.
Cornelia A. Van Cott, Math Horizons, 23 (2016) no. 3, 24 – 27.
Abstract: Most of your mathematical life, you've known that pi is an irrational number somewhere between 3.1 and 3.2. But if we exchange the usual notion of distance for other notions, pi can be any of an infinite number of different values.
The Mathematical Association of America awarded this paper the 2017 Trevor Evans Award.
Here is a video of a talk I gave on this topic.
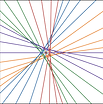
Megan Martin, Cornelia A. Van Cott, Qiyu Zhang. Math Horizons, 31 (2024) no. 2, 14 - 17.
Abstract: In his notebook margins, Pierre de Fermat scribbled conjectures which famously led to deep mathematical discoveries. The rest of us are more likely to doodle stars, hearts, emojis, and anime characters in our notebook margins. But, once in a while, even doodles and drawings give rise to mathematical adventures. We take on one such doodling challenge and investigate what happens when we draw all lines that slice the area of a polygon in half. This leads us down a path filled with beautiful pictures and interesting mathematics.
The Mathematical Association of America awarded this paper the 2024 Trevor Evans Award.
Editorials
Giving Talks for Undergraduates
Notices of the American Mathematical Society, November 2024.